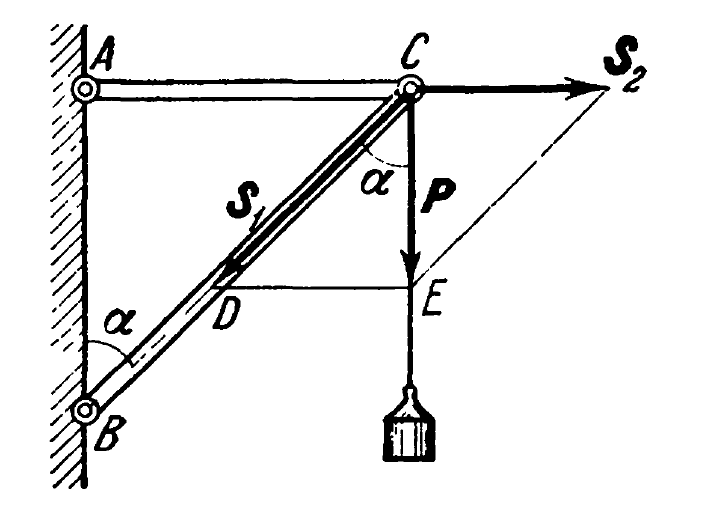
The Law of Sines is a powerful tool in 2D vector analysis. The problem (illustrated above) is taken from Targ (1988). The Law of Sines is illustrated below.

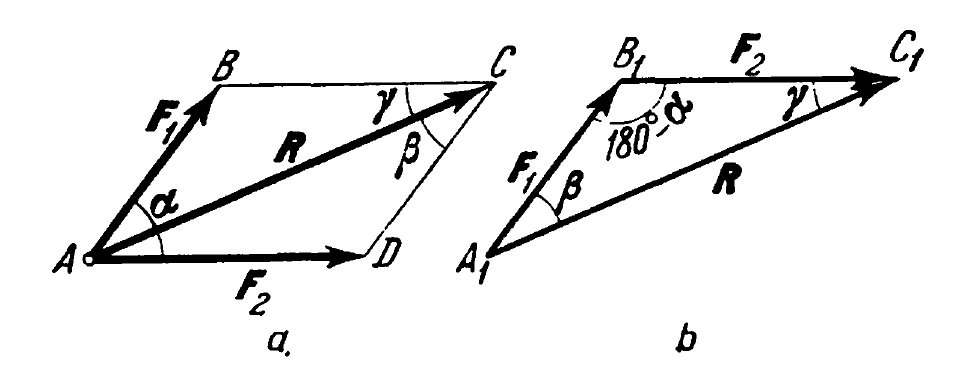
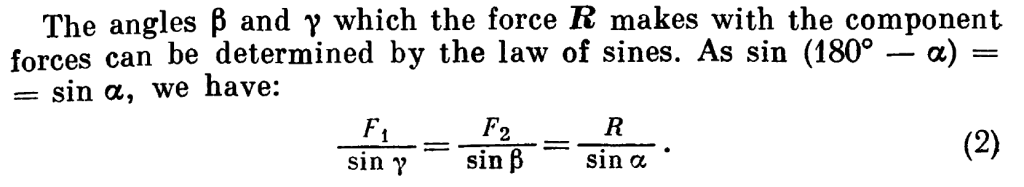
Our goal is to find the force components S1 and S2 using the Law of Sines. We first note that we have a right triangle, thus β = 90° – α and γ = 90°. We move the vector S2 down to DE to make a force triangle. From the Law of Sines,

\frac{P}{\sin(\beta)} = \frac{S_1}{\sin(\gamma)} = \frac{S_2}{\sin(\alpha)} (1)

(As long as our designation of the angles and their corresponding sides is consistent, the Law of Sines holds.)

Noting that sin(β) = sin(90° – α)=cos(α) and sin(γ)=1,

S_1 = \frac{P}{\cos(\alpha)} (2)

We can also say that

S_2 = P \tan(\alpha) (3)

As an example, consider the case of P = 10 kN and α = 60°. By substitution into Equations (2) and (3), S1 = 20 kN and S2 = 5.77 kN.

Further question: what happens as we vary the value of α?