The mass moment of inertia of a cylinder with uniform thickness (square ends) is an elementary problem in engineering mechanics. But it’s also a good way of illustrating the relationship between the mass moment of inertia and the rotational moment of inertia, both of which are discussed in Two Papers on Vibratory and Impact-Vibration Hammers. There are two methods we can use: a) direct integration of the volume/mass and b) area rotational moment of inertia which can, under certain circumstances, can be used to determine the mass moment of inertia.

Direct Integration of the Volume/Mass

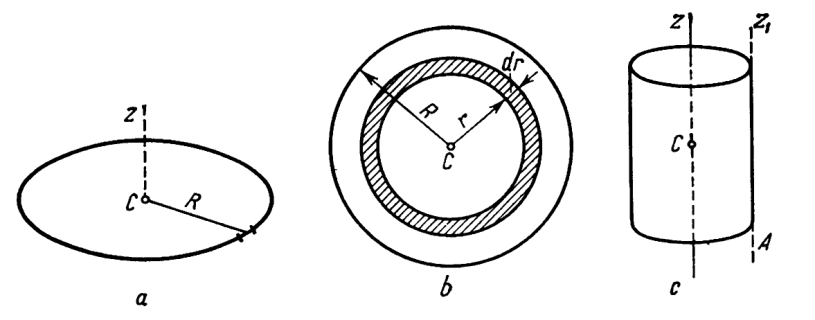
A diagram of the cylinder is shown above, from Targ (1988). We start with the integration formula thus, using (b) in the diagram above for the entire volume (c):

{\it Iz}=\rho\,\int _{0}^{t}\int _{0}^{2\,\pi }\int _{0}^{R}{r}^{3}{dr}\,{d\theta}\,{dz} (1)

Integrating,

{\it Iz}=1/2\,\rho\,t\pi \,{R}^{4} (2)

Note that, in this form, it is unnecessary to compute the mass of the cylinder before the mass moment of inertia.

Using the Area Rotational Moment of Inertia

The integral formula for just the circular area (a) in the diagram above is given using the formula

{\it J_0}=\int _{0}^{2\,\pi }\int _{0}^{R}{r}^{3}{dr}\,{d\theta} (3)

If we compare this with Equation (1), we note the similarity. In fact, if a) the density \rho is constant and b) the thickness t is also constant, the two are the same. These are the conditions under which the area moment of inertia can be used to compute the mass moment of inertia. Performing the integration,

{\it J_0}=1/2\,\pi \,{R}^{4} (4)

For the very specific conditions given above, either from dividing Equations (1) and (3) or Equations (2) and (4),

I_z = \rho t J_0 (5)

As is the case in this post, composite areas are volumes are used to compute the mass moment of inertia. If the conditions are as noted above, area moments of inertia (which are more commonly tabulated) can be used to compute mass moments of inertia.