Determining the Centroid, Moment of Inertia and Radius of Gyration of an Area

This is an expansion of a problem from Targ (1988) on this subject, which comes into play in both Statics and Mechanics of Materials.

Let us begin by considering the area in question; the dimensions are in centimetres.

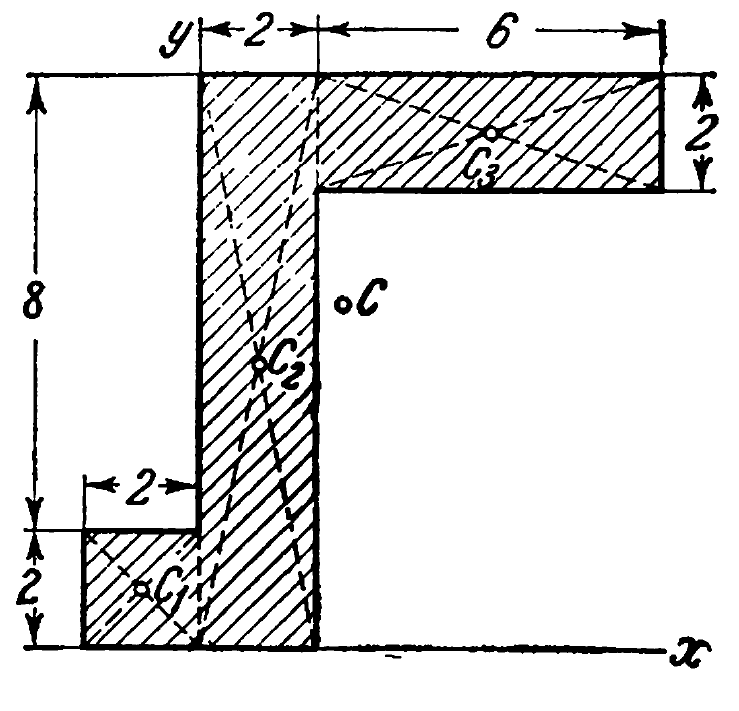
The first thing we will do is determine the centroid of the entire system. We do this by determining the centroid of each part of the section and then determining the centroid of the entire system using a weighted average. A similar procedure is employed in Determining the Eccentric Moment, Rotational Inertia and Pendulum Frequency for a Vibratory Eccentric.

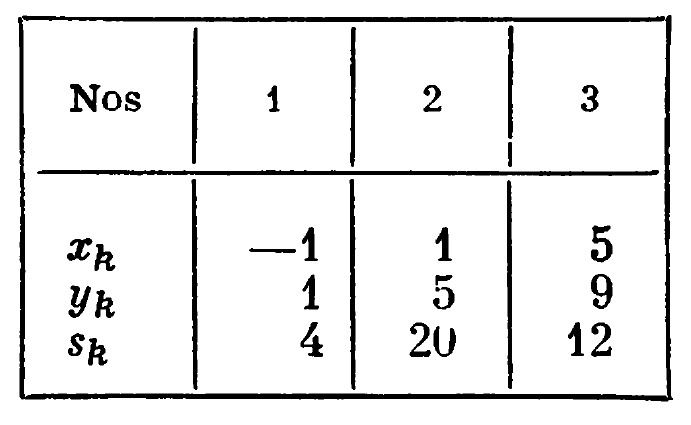
The area and the coordinates of the centroids for each section are noted in the table at the right. Each of these centroids is relative to the coordinate system shown in the diagram above.

The centroid is determined as follows:

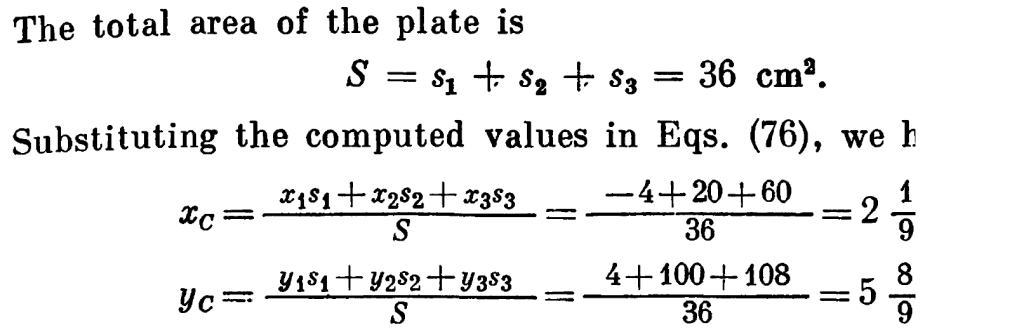
Now we turn to the matter of the moment of inertia. The moment of inertia for a rectangle is given by the equation

$I = \frac{bh^3}{12}$ (1)

But this equation needs to be understood as follows:

The base b is the side of the rectangle which is parallel to the axis around which the moment of inertia is being taken. So, for Area 2, for I_x, b = 2, as the short side is parallel to the x-axis.
The height h is the side of the rectangle which is perpendicular to the axis around which the moment of inertia is being taken. So, for Area 2, for I_x, h = 8, as the long side is perpendicular to the x-axis.
For the moment of inertia I_y, you simply switch b and h.
The moment of inertia computed with Equation (1) for rectangles is for an axis system with the origin a the centroid of the rectangle. To find the moment of inertia around another point/axis system, you need the parallel axis theorem.

And this is where things get a little tricky. The formulas for this transformation in a Cartesian system is given as follows:

$I_x = I_{x0} + d_y^2 A$ (2a)

$I_y = I_{y0} + d_x^2 A$ (2b)

where $I_x,\,I_y$ are the transformed moments of inertia about the new coordinate system and $I_{x0},\,I_{y0}$ are the original moments of inertia (in this case around the centroid.) The variable $A$ is the area of the section (or part of the section) and $d_x,\,d_y$ are the distances along the axes from the original to the new coordinate system.

The hard part is understanding why the reversal in Equations (2a) and (2b) between the moments of inertia and values of $d$ . The answer to that question is best shown in an illustration.

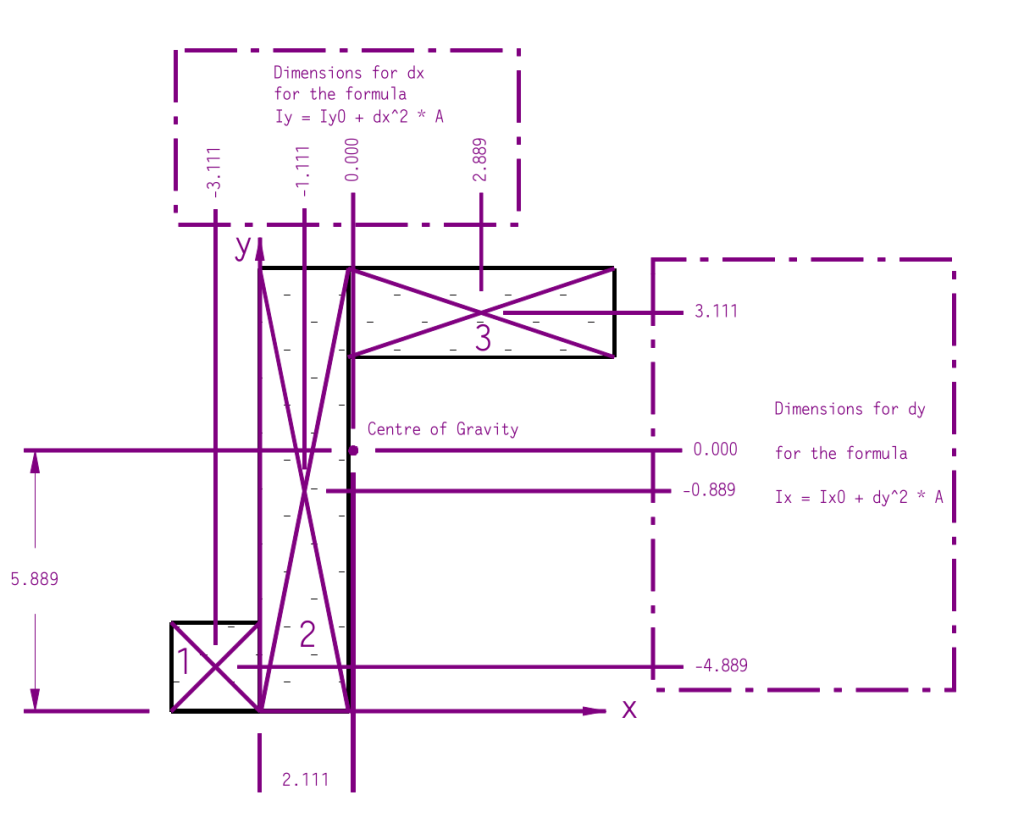
The value I_x means that the moment of inertia is taken around the x-axis, not in the direction of the x-axis. Thus the shifts in coordinates for the x-axis moment of inertia take place in the y-direction and vice versa.

To obtain the result we simply make this transformation for each section and add up the I_x and I_y values that result. This is shown in the table below. The table is split up for formatting purposes.

Area	b	h	Area Centroid Distance from x-axis, cm	Area Centroid Distance from y-axis, cm	Area I_x Centroid of Section, cm⁴	Area I_y Centroid of Section, cm⁴
1	2	2	1	-1	1.333	1.333
2	2	10	5	1	166.667	6.667
3	6	2	9	5	4.000	36.000

Centroid x coordinate	2.111
Centroid y coordinate	5.889

Area	Area, cm^2	d_y for Parallel Axis Theorem, cm	d_x for Parallel Axis Theorem, cm	I_x of Area around Total Centroid, cm⁴	I_y of Area around Total Centroid, cm⁴
1	4	-4.889	-3.111	96.938	40.049
2	20	-0.889	-1.111	182.469	31.358
3	12	3.111	2.889	120.148	136.148
Total Area, cm²	36		Total I, cm⁴	399.556	207.556
			Radius of Gyration, cm	3.331	2.401