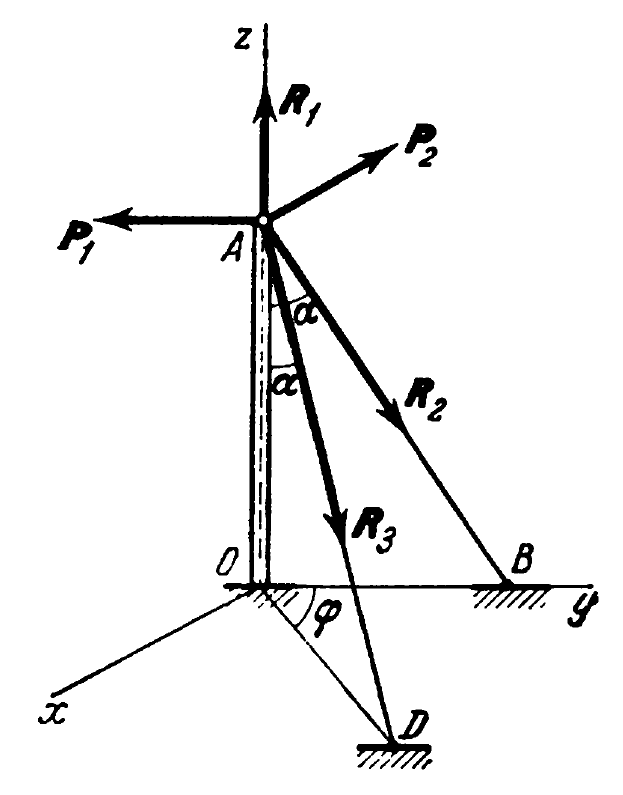
This is an example of the computation of forces on a single point, given some of the forces on the point. The example is taken from Targ (1988). The problem concerns the forces at the tip of the pole shown at the right. Details are as follows:
- Pole problem as shown on the right
- Force P1 is parallel to y-axis with a magnitude of -1 kN
- Force P2 is parallel to x-axis with a magnitude of -1 kN
- Reactions R2 and R3 are inclined from the pole by α = 30 deg.
- Point B is along the y-axis
- Point D is inclined at an angle φ = 60 deg. From the y-axis
The goal is to find reactions R1, R2 and R3.
We proceed as follows:
- Since P1 is parallel to the y-axis, P1 = -1j
- Since P2 is parallel to the x-axis, P2 = -1i
- Let us assume the pole is L m long. That being the case, Point A has coordinates of (0,0,L) and Point O (0,0,0)
- Since α = 30 deg., the distance OB = OD = (3)½ L
- Since Point B is along the y-axis, it has coordinates of (0,(3)½ L,0)
- Point D is 30 deg. off of the x-axis and distance (3)½ L from O, thus its coordinates are (½ L, L/(2(3)½), 0)
- In decimals, the points are as follows:
- A (0,0,L)
- B ((0, 0.5773L, 0)
- D (0.5 L, 0.2887L, 0)
- Position Vectors of AD and AB:
- AD = (0.5-0)Li + (.2887-0)Lj + (0-1)Lk = L(0.5i + .2887j – 1k)
- AB = (0-0)Li + (.5773-0)Lj + (0-1)Lk = L(.5773j – 1k)
- Moduli/Length of Vectors:
- AD = AB = 1.15 L = 2/(3)½ L
- Unit Vectors for AD and AB: (Unit vectors are explained in the post The Tripod Problem: An Example of Vector Forces)
- ad = L(0.5i + .2887j – 1k)/1.15L = 0.4347i + 0.2510j – 0.8696k
- ab = L(.5773j – 1k)/1.15L = 0.502j – .8696k
- Equations for Reaction and Force Vectors
- R1 = R1k
- R2 = R3(0.502j – .8696k)
- R3 = R2(0.4347i + 0.2510j – 0.8696k)
- P1 = -1j
- P2 = -1i
- Summing the Force and Reaction Vectors to Zero
- ΣF = 0 = (.4347R3 – 1)i + (0.502R2 + .2510R3 -1)j + (R1 – .8696R2 – 0.8696R3)k
- Solving i first, R3 = 2.3 kN
- Solving j next, R2 = 0.842 kN
- Solving k last, R1 = 2.732 kN
Solving Using Linear Algebra
The problem can also be solved using linear algebra, as was the case in the post Solving a Statics Problem Using Linear Algebra. Taking the last summation of forces and putting it into matrix form, we have

The reactions were arranged to make the matrix lower triangular, which means that inversion was unnecessary, as the system could be solved using forward substitution (which, in reality, is what we did above.) The result, as we would expect, is the same.