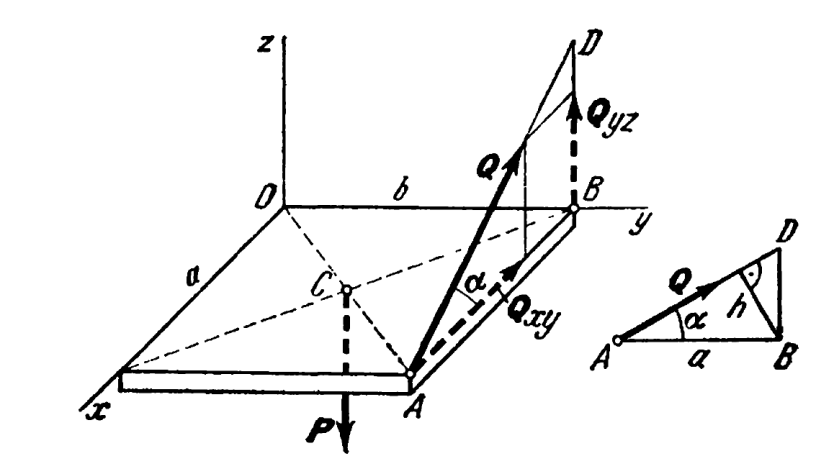
This is an example of the vector triple product, where we compute the moment in a certain direction of interest. The example comes from Targ (1988) but the application is very different.
Consider the problem below, with the force P on the plate.
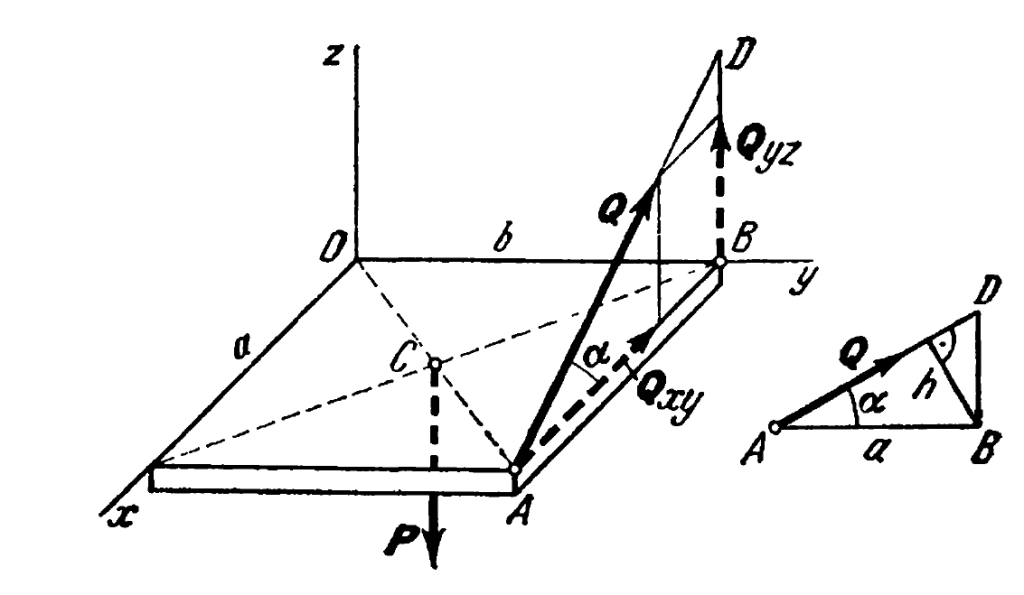
The object is to determine the moment of the force P around the point A (which is in the line of action of the line Q) in the direction of Q. We can do this in one of two ways: a)application of the cross product to determine the moment and then the dot product to determine the moment in the direction of interest and b)application of the vector triple product to obtain the same result.
The moment arm from A to C has the position vector
(1)
The force vector is given as
(2)
The vector cross product of the moment at A is
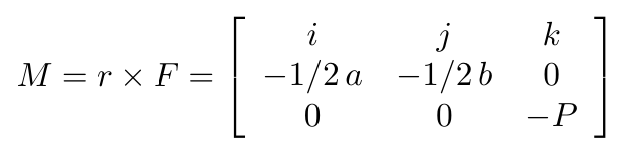
The determinant of this cross product is
(4)
The unit vector of Q is straightforward to determine since the vector is entirely within the x-z plane. It is
(5)
The dot product of this unit vector and the moment (the projection of the moment on Q) is
(6)
We can also use the vector triple product directly to obtain the same result. The cross product is determined using the matrix (from Equations (1), (2) and (5)) as
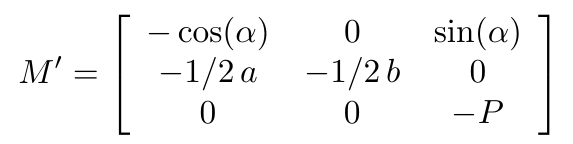
The determinant of this is
(8)
which is the same result.