In this problem we will look at analysing a loaded beam for its reactions. We will use a free body diagram to accomplish this. This problem is taken from Movnin and Izrayelit (1970).
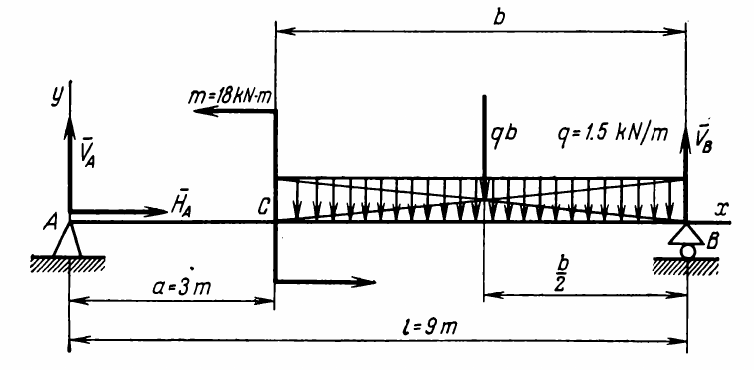
Consider the beam above, with b = 6 m. We need to determine the reactions VA, HA and VB. First the free body diagram is the entire beam with the boundary at the reactions. From there we proceed as follows:
- We first concentrate the distributed load qb to a concentrated QB = (6)(1.5) = 9 kN, which is b/2 = 3 m from B or 6 m from A.
- There are no forces in the x direction, thus HA = 0.
- We will take moments around A to determine VB.
- Sum of moments around A is as follows: 18 – (6)(9) + (9)VB = 0. Solving for VB, VB = 4 kN.
- We now sum the forces in the y-direction, thus: VA – 9 + 4 = 0. Solving for VA, VA = 5 kN.
As is the case with many (but not all) problems like this, it is better to start with the summation of moments and then compute the summation of forces.