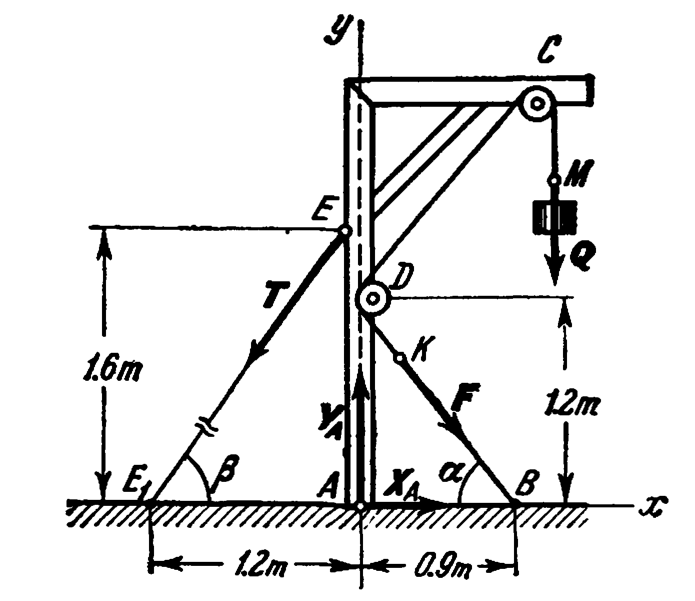
This is an example of the analysis of the structure/mechanism shown above. It is taken from Targ (1988). A weight Q of 2400 N is suspended at Point C. Neglecting the weight of the frame, sheaves and cables, the object of the analysis is to determine the reactions shown at Points A, E1 and B. The distance from the y-axis to Point C is 1m and the other dimensions are shown.
Let us begin by determining the angles α and β. First α, which is determined by the equation
tan(α) = 1.2/0.9 (1)
which solves to
α = .927 radians = 53.13 degrees (2)
In like fashion,
tan(β) = 1.6/1.2 (3)
and
β = .927 radians = 53.13 degrees (4)
The two angles are thus the same. Closer inspection will reveal that the triangles that define these forces are in fact the classic “3/4/5” triangles.
Summation of forces in the x-direction is
XA + F cos(α) – T cos(β)=0 (5a)
which substituting becomes
XA + .6 F − .6 T = 0 (5b)
For the y-direction forces,
YA – F sin(α) – T sin(β) – Q = 0 (6a)
and substituting
YA − .8 F − .8 T − Q = 0 (6b)
At this point we need to sum the moments. Point A is the best place to do this; this takes the reactions there out of the equation. Additionally the connection is pinned at this point, so the moment there is zero. We could use vector notation, but in this case we will resort to “old coot” methods. We can pick any point along the line of action of the two forces F and Q. We will pick the points where the two cables meet the ground, i.e., the reaction points. As a result neither of the x-direction components of the two forces enters into play because both the line of action of both of these components pass through the point A. Only the y-direction components count, and the x-distances from point A to point E1 (T) and V (F) are the moment arms. The y-direction forces can be taken from Equation (6) above. This is illustrated below.

Taking the moments and mindful of their signs, the summation of moments is thus:
.96 T − .72 F − 1. Q = 0 (7)
Note that the moment of Q around the y-axis is included. Since we have brought the subject of Q up, we can note that, because the sheaves are frictionless, the cord transmits the force of the weight perfectly, thus
F = Q (8)
Substituting Equation (8) into Equations (5), (6) and (7) and equating Q = 2400 N yields
XA + 1440. − .6 T = 0 (9a)
YA − 4320. − .8 T = 0 (9b)
0.96 T − 4128 = 0 (9c)
Solving Equation (9c) first for T and then the other two equations for the other two variables, we have at last
T = 4300 N
XA = 1140 N
YA = 7760 N