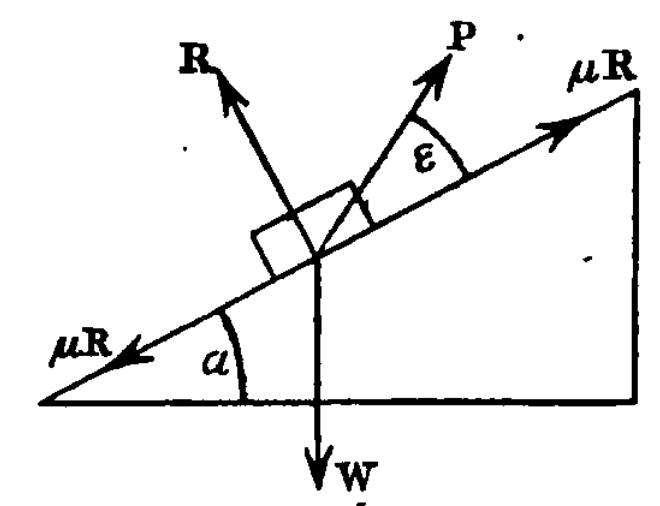
A block on a slope with an inclination of α = 30 degrees is shown at the right. The block has a weight W = 10 kN. The force R is the net normal force on the block. The forces μR are the frictional forces; which direction is valid depends upon the action of the other forces; μ = 0.4. A force P acts at an angle ε = 15 degrees from the surface of the slope. Determine the value of P at the point of impending motion of the block up the slope.
There are two things to note right up front that will make this problem simpler:
- The coordinate system should be set up with the x-axis parallel to the slope and upwards and the y-axis normal to the slope in the direction of the block’s normal force R.
- Since the problem specifies that the impending motion of the block is up the slope, the component μR we will use is the one pointing downward on the slope.
With all that said, taking a free body diagram of the block itself, the summation of the forces in the x-direction is
P cos ε – μR – W sin α = 0
and in the y-direction
P sin ε + R – W cos α = 0
If we solve both equations for R, equate the results to each other and then solve for P, we have
P = W (sin α + μ cos α) / (cos ε + μ sin ε)
Substituting the values given yields P = 7.9 kN.
The solution in Smith’s Mechanic for this problem–in both directions of possible impending motion–is at the top.
