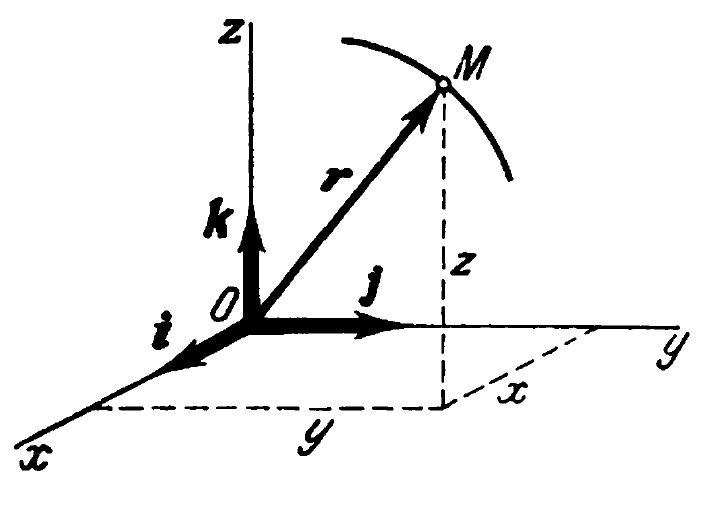Refer to the diagram above. The position of a particle in motion is defined by the vector r(t) (we’ll include its dependence on time for clarity) with respect to some coordinate system/frame of reference. We proceed as follows:
- Displacement
- Vector:
(1)
- Scalar magnitude:
(2)
- Vector:
- Velocity (first derivative of displacement)
- Vector:
(3)
- Scalar magnitude:
(4)
- Vector:
- Acceleration (first derivative of velocity, second derivative of displacement)
- Vector:
(5)
- Scalar magnitude:
(6)
- Vector:
Now let us look at an example. The motion is defined by the time dependent quantities . Substituting these into the equations above yields the following:
- Displacement
- Vector:
- Scalar magnitude:
- Vector:
- Velocity (first derivative of displacement)
- Vector:
- Scalar magnitude:
- Vector:
- Acceleration (first derivative of velocity, second derivativ
- Vector:
- Scalar magnitude:
- Vector: