Impulse, Momentum, Artillery and Recoil: An Example

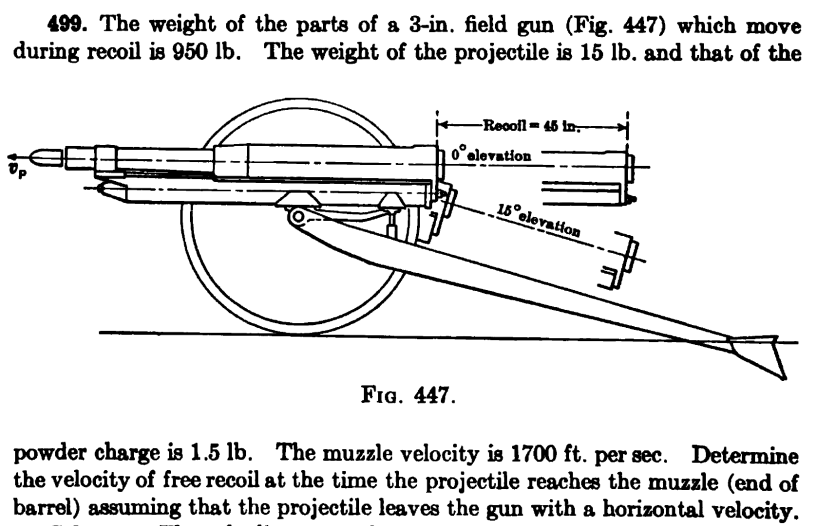
Visitors to this site’s “main” theme know that it centres around my grandfather’s life and career. An important event in his time here was World War I, and one of the things that was central to that conflict was artillery. This problem comes from Seely and Ensign (1921) and concerns artillery and recoil. Artillery is still important, as evidenced by the war in Ukraine, and it’s a fairly straightforward example of the conservation of impulse and momentum.

The problem is stated and illustrated above. We note this up front:

• Artillery are equipped with a recoil damper that slows the barrel down; we are interested in the velocity at the time the projectile leaves the muzzle.
• We assume the powder charge follows the projectile at half the projectile’s velocity.

Conservation of momentum dictates that the total momentum of the system of particles without an external force is unchanged from before firing until after the projectile leaves the muzzle. This is expressed as

ΣI = Σm_nV_n = 0 (since all initial velocities are zero) (1)

Summation immediately after projectile leaves muzzle:

m_pv_p + m_gv_g + m_rv_r = 0 (all in x-direction) (2)

Substituting (note the negative velocities of the projectile and gas,)

(15)(-1700) + (1.5)(-1700/2) + 950v_r = 0 (dividing through by g_c) (3)

Solving,

v_r = 28.2 ft/sec (4)

An additional problem is to find relative velocity of the projectile to the barrel at exit. Using the relative velocity equation,

v_p = v_r + v_p/r (5)

Solving for the relative velocity,

v_p/r = v_p – v_r = 1700 – (-28.2) = 1728.8 ft/sec (6)

A more complete example of velocity relative to a moving coordinate system is given in the post Relative Motion, or Making Sure You’re Getting Where You’re Going.