The instantaneous centre of zero velocity (better characterised as the instantaneous centre of rotation) is a holdover from the days of graphical analysis. It does provide a powerful tool to analyse the motion of rigid bodies. First an explanation of this is given, from Movnin and Izrayelit (1970):

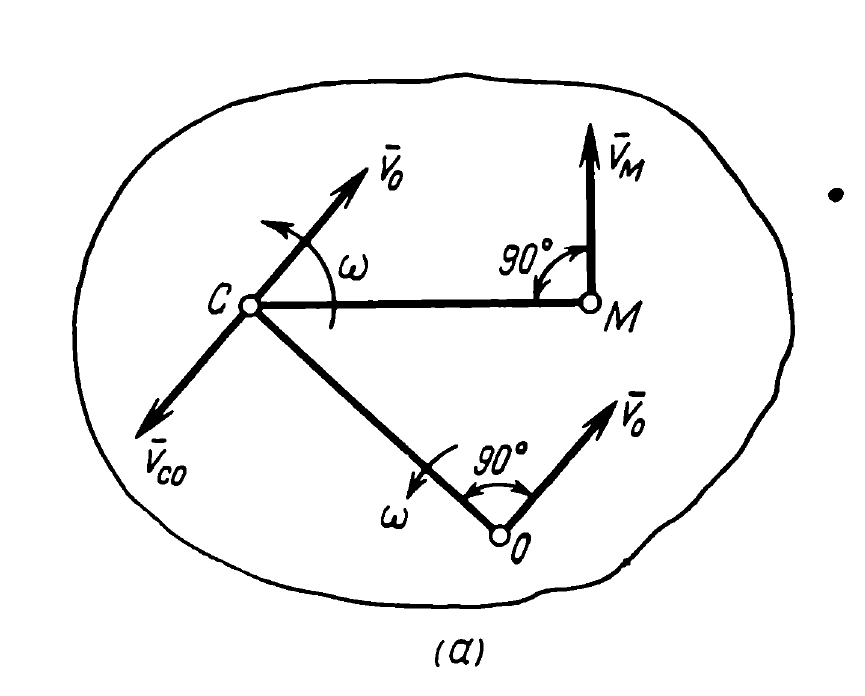




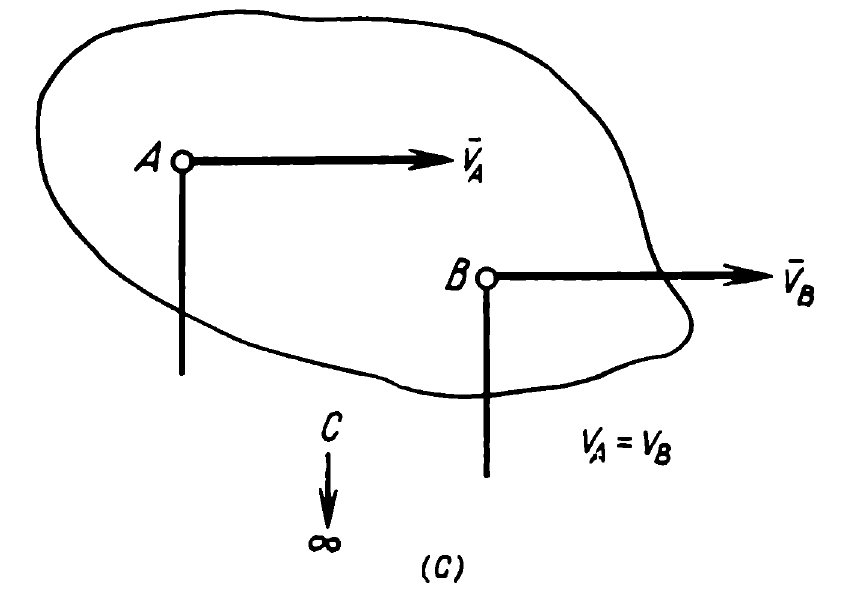

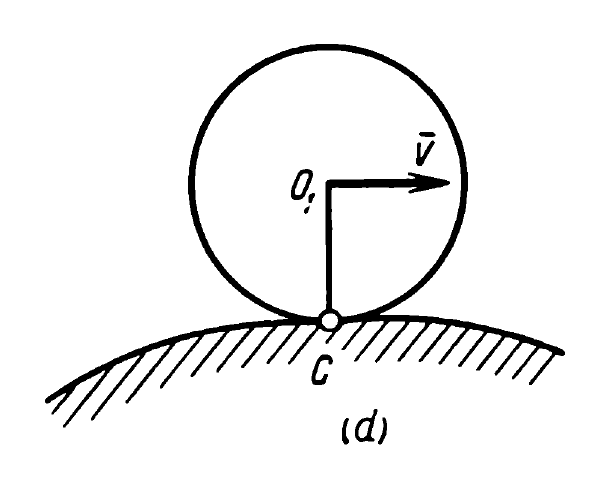



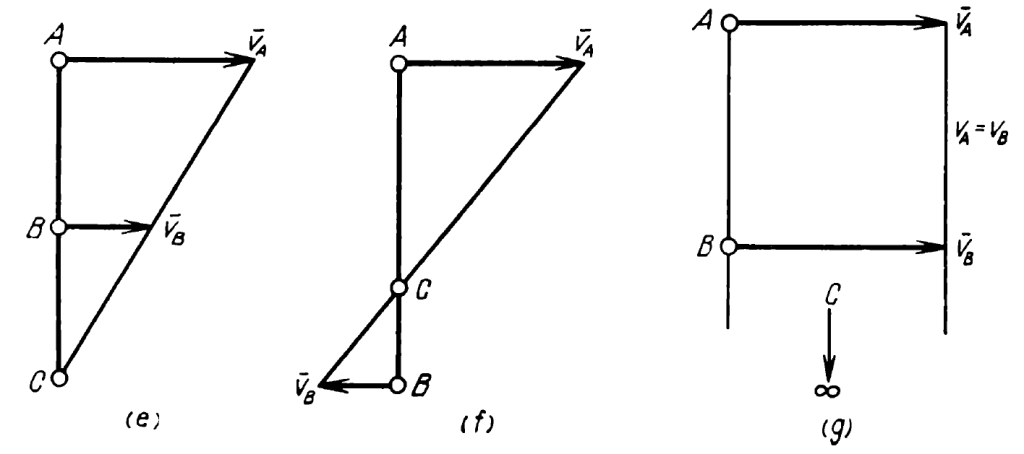
Now for two examples.
The first involves the mechanism shown below. In this mechanism VA = 1.5 m/sec and α = 30 deg. We need to find VB.

We have two points with two velocities; thus, the centre of rotation is at the intersection of the two perpendicular velocities (Point C, Case 1.) We can thus compute the instantaneous angular velocity ω = 1.5/AC (v = rω.) Also true is ω = VB/BC.
- By geometry, BC/AC = tan(30), or BC/AC = 0.577
- 1.5/AC = VB/BC
- VB = 1.5*BC/AC = 1.5.577 = 0.866 m/sec
The second example is the Wheel as shown below, rolling without slippage. R = 0.5 m and Vo = 2 m/sec. Find the velocities at points M1, M2, M3 and M4.
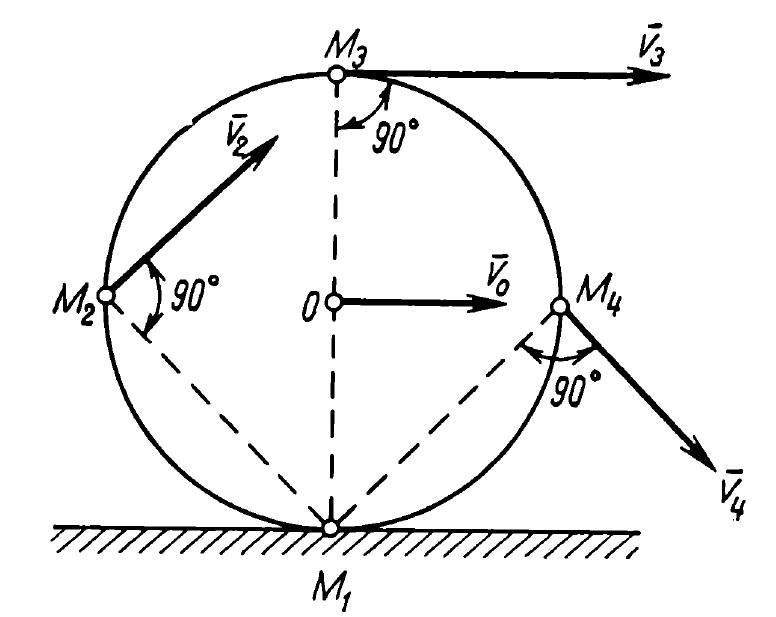
We proceed as follows:
- Instantaneous centre of rotation is at point M1 because it is fixed to the ground at that instant, thus V1 = 0 (Case 2)
- Thus ω = v/r = 2/0.5 = 4 rad/sec
- Radius of rotation for Points 2 and 4 is the same = r/sin 45 = 0.5/.707 = .707 m, thus V2 = V4 = .707*4 = 2.83 m/sec in direction as shown
- Radius of rotation for Point 3 is simply 2r = 1m, thus V3 = 1*4 = 4 m/sec in the direction shown
More examples are available in Movnin and Izrayelit (1970).