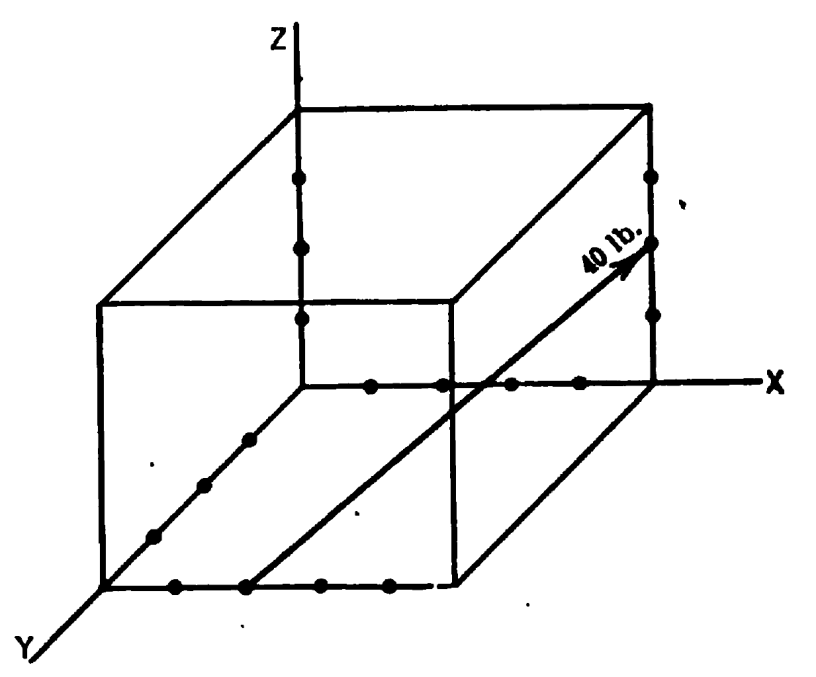
Vector cross-products are at the centre of statics these days, and can even be applied to problems such as this one. Their best application is with 3D problems such as this one, from Seely and Ensign (1921). Although vectors were not generally taught at the time, they definitely make the problem simpler to solve. This problem is also a good example of the “line of action” of a force; if you can define a position vector from the moment point desired, any vector from that point to the line of action will yield the same result.

The problem is illustrated above. The original problem statement asked to “Find the moment of the 40 lb. force with respect to each of the coordinate axes; each division represents 1 in.” To obtain a vector representation of the moment actually fulfils this requirement.

The first thing we need to do is to determine the force vector. This is done by first determining the unit vector of the force, which is

{\it u_1}=1/29\,\left (3\,i-4\,j+2\,k\right )\sqrt {29} (1)

We then multiply this by the scalar magnitude of the vector for the complete force vector, which is

{\it F_1}={\frac {40}{29}}\,\left (3\,i-4\,j+2\,k\right )\sqrt {29} (2)

or in floating point form,

{\it F_1}= 22.28344058\,i- 29.71125411\,j+ 14.85562705\,k (2a)

This is the same force for both of the moment arms we will consider.

The first moment arm is the one from the origin to the point where the line of action of the force crosses the front of the box, namely

{\it r_1}=2\,i+4\,j (3)

The cross product is thus

r_1 \times F_1 = \left [\begin {array}{ccc} i&j&k\\{\medskip}2&4&0\\{\medskip}{\frac {120}{29}}\,\sqrt {29}&-{\frac {160}{29}}\,\sqrt {29}&{\frac {80}{29}}\,\sqrt {29}\end {array}\right ] ={\frac {320}{29}}\,i\sqrt {29}-{\frac {160}{29}}\,j\sqrt {29}-{\frac {800}{29}}\,k\sqrt {29} (4)

or in floating point representation

59.42250822\,i- 29.71125411\,j- 148.5562706\,k (4a)

This indicates that the moment around the x-axis is 59.4 in-lb counter-clockwise, around the y-axis -29.7 in-lb clockwise, and 148.6 in-lb clockwise around the z-axis. The signs were used to determine the rotation of the moments.

We can also use the position vector at the point where the force line of action crosses the back of the box, namely

{\it r_2}=5\,i+2\,k (5)

Since the force vector is identical, the cross-product is

r_2 \times F_1 = \left [\begin {array}{ccc} i&j&k\\{\medskip}5&0&2\\{\medskip}{\frac {120}{29}}\,\sqrt {29}&-{\frac {160}{29}}\,\sqrt {29}&{\frac {80}{29}}\,\sqrt {29}\end {array}\right ] ={\frac {320}{29}}\,i\sqrt {29}-{\frac {160}{29}}\,j\sqrt {29}-{\frac {800}{29}}\,k\sqrt {29} (6)

which is identical to the result of Equation (4), thus the floating point representation is the same as Equation (4a). This is a demonstration of the “line of action” principle, in that two different moment arms along the same line of action produced the same moment.