Two Examples of Vector Addition

In my series for my Statics class, we have two examples of vector addition. Both of these are taken from (with some modification) from Levinson.

The first (shown at the right) concerns two forces P₁ and P₂ which are each 60 degrees from the positive x-axis (OC) but on opposite sides. Assuming that P₁ = P₂, determine the value of the resultant R. Do this in two ways: with “old coot” methods and with formal vector analysis.

In either case we need to break up the vectors into their components. For an angle α those components are as follows:

P_x = P cos (α) (1a)

P_y = P cos (90 – α) (1b)

The angle α is the counterclockwise angle from the positive x-axis. This is crucial; doing this is intended to prevent you from getting lost in the quadrants. The y-component can be expressed otherwise but why we do this here is better explained when we discuss direction cosines.

In any case computing the x- and y-components and solving the problem is fairly straightforward, as follows:

α₁ = 60 degrees
α₂ = 360 – 60 = 300 degrees
P_x1 = P cos (60) = 0.5 P
P_y1 = P cos (90 – 60) = 0.866 P
P_x1 = P cos (300) = 0.5 P
P_y1 = P cos (90 – 300) = -0.866 P
It should be evident that the x-axis forces add and the y-axis forces cancel each other, thus R = P and α_R = 0

Let’s transition to formal vector notation with this, from Strelkov:

In our notation formal vector expression looks like this in two dimensions:

P_n = P_n cos (α_n) i + P_n cos (90 – α_n) j (2)

The vectors i and j are the unit vectors in the x- and y-direction respectively. The quantities in bold are vector quantities. Some posts use a different notation.

Since we have already computed the coefficients, the vectors are as follows:

P₁ = P cos (60) i + P cos (90 – 60) j = 0.5 P i + 0.866 P j
P₂ = P cos (300) i + P cos (90 – 300) j = 0.5 P i – 0.866 P j

In vector addition (and subtraction for that matter) we add or subtract the i and j separately. Doing this means in this case the i components add and the j components cancel each other out, leaving us with

R = P₁ + P₂ = P i

The second problem is at the right. The vectors are concurrent forces at a point as follows:

P₁ = 0.23 kN, α₁ = 26 degrees
P₂ = 0.275 kN, α₂ = 68 degrees
P₃ = 0.213 kN, α₃ = 15 degrees
P₄ = 0.3 kN, α₄ = 59 degrees
P₅ = 0.3 kN, α₅ = 31 degrees

We must determine whether system is in equilibrium at Point 0, using both methods of vector analysis. As before, For conditions of static equilibrium, forces at 0 must sum to zero in a vector sense, thus the sum of all P = 0.

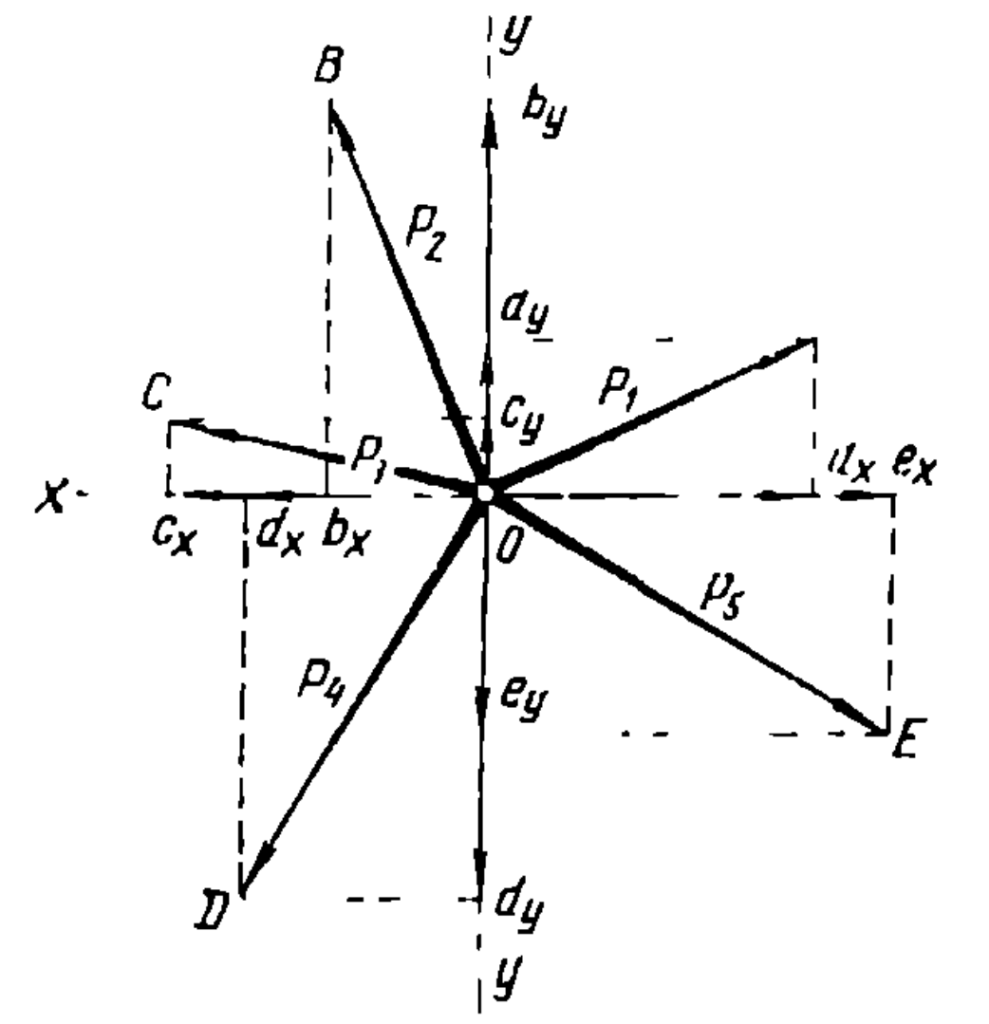
Since these are vector quantities, the forces in the x-direction and the forces in the y-direction must both equal zero, or (see diagram at left)

a_x + b_x + c_x + d_x + e_x = 0
P_1x + P_2x + P_3x + P_4x + P_5x = 0
a_y + b_y + c_y + d_y + e_y = 0
P_1y + P_2y + P_3y + P_4y + P_5y = 0

The angles of each force should be defined in a counterclockwise direction from the positive x-axis so the signs of the components will be correct, thus the input data for this problem is as follows:

Force	Scalar Magnitude, kN	Angle from x-axis on drawing, degrees	Angle from positive x-axis α, degrees	Angle from x-axis α, radians
1	0.23	26	26	0.4538
2	0.275	68	112	1.9548
3	0.213	15	165	2.8798
4	0.3	59	239	4.1713
5	0.3	31	329	5.7421

The components of the forces are computed from Equations (1a) and (1b). For example, considering force P₄,

The cosines are as follows: cos α_n = −0.515 and cos (90-α_n) = −0.857
The forces are P_4x = (0.3)(-.515) = -0.1545 and P_4y = (0.3)(-0.857) = -0.2572

If we repeat this for all of the forces, the results are as follows:

Force	Scalar Magnitude, kN	Angle from x-axis on drawing, degrees	Angle from positive x-axis, degrees	Angle from x-axis, radians	X-direction component, kN	Y-direction Component, kN
1	0.23	26	26	0.4538	0.2067	0.1008
2	0.275	68	112	1.9548	-0.1030	0.2550
3	0.213	15	165	2.8798	-0.2057	0.0551
4	0.3	59	239	4.1713	-0.1545	-0.2572
5	0.3	31	329	5.7421	0.2572	-0.1545
				Sums	0.001	-0.001

We can see that the sums are very small, thus for practical purposes the point O is in equilibrium.

For the formal vector solution, we have done most of the hard work because we have identified the x- and y- components of each force. We use the unit vectors i (x-direction) and j (y-direction) to designate the components. We thus write the vector forces as follows:

P₁ = 0.2067 i + 0.1008 j
P₂ = -0.1030 i + 0.2550 j
P₃ = -0.2057 i + 0.0551 j
P₄ = -0.1545 i – 0.2572 j
P₅ = 0.2572 i – 0.1545 j

To obtain the net force on Point 0, we simply add the i forces (x-direction) and j forces (y-direction) to check

ΣP_x = 0.2067 i – 0.1030 i -0.2057 i – 0.1545 i + 0.2572 i ~ 0
ΣP_y = 0.1008 j + 0.2550 j + 0.0551 j – 0.2572 j – 0.1545 j ~ 0

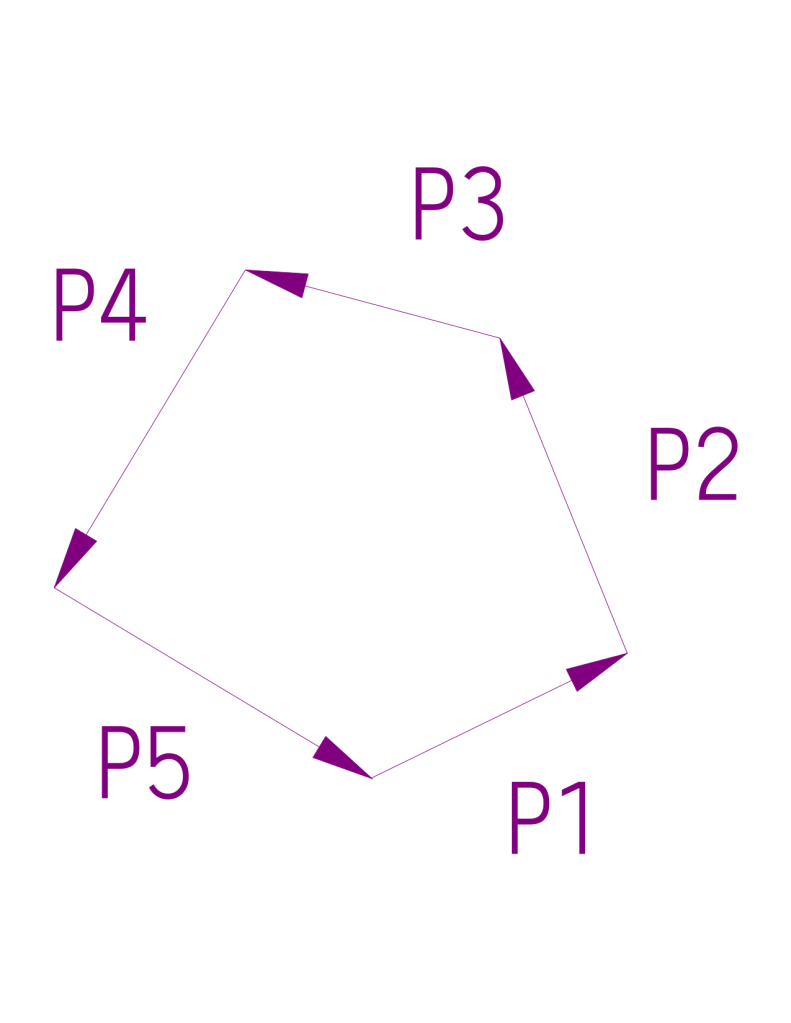
After these things I decided to do this problem graphically on CAD. By simply going from one force to another with the magnitude and direction, I came up with this diagram, which shows that the resolution of the forces is very small.

Notes

In vector addition and subtraction, do not mix different direction components, such as i forces with j forces.
The components of the forces are also referred to as the projections of the vectors on the x- or y-axis.
Although there is little advantage to using vector notation in this problem, with three-dimensional problems of greater complexity it is better.

Example of Dot Product

We can also use this to illustrate the use of the dot product, which is described below.

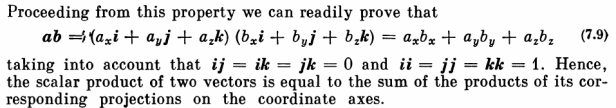
Consider the vectors P₁ and P₂. Determine the following:

Dot Product of P₁ and P₂
Angle between P₁ and P₂

The vectors are given above. We want to use Equation (7.9) to determine the actual dot product and Equation (7.8) to determine the angle. Starting with (7.8,)

(.2067)(-0.1030)+(.1008)(.2550) = (0.23)(0.275) cos α_1-2

The left hand side is the dot product according to Equation (7.9,) or 0.0044139. On the right hand side P₁ P₂ = 0.06325. The angle between them α_1-2 = arccos (0.0044139/0.06325) = 86 degrees. This can be checked against the given geometry and shown to be correct.