Solving a Statics Problem Using Linear Algebra

Engineering students have been solving statics problems for generations by a process of elimination for two or three equations. This is a demonstration (certainly not unique) of a solution using linear algebra. Most engineering students now have had linear algebra early in their studies, which was not the case in the past. The problem is taken from Movnin and Izrayelit (1970).

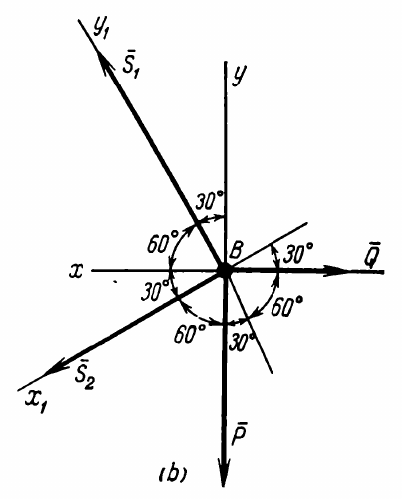
The problem can be stated as follows:

The solution is as follows:

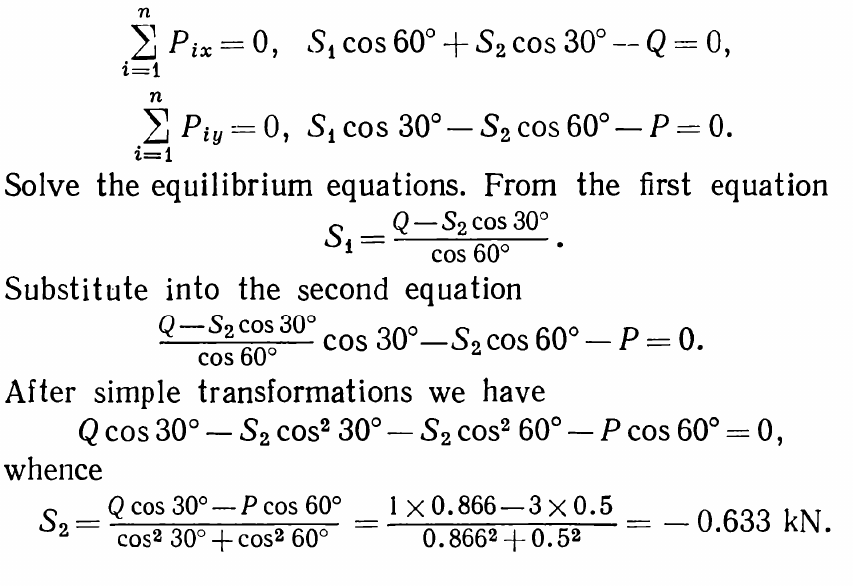
Turning to linear algebra, the solution can be put in the classic form

$Ax=b$ (1)

We transform the equations (with the cosines substituted)

$1/2\,{\it S_1}+1/2\,{\it S_2}\,\sqrt{3}-Q =0$ (2a)
$1/2\,{\it S_1}\,\sqrt{3}-1/2\,{\it S_2}-P =0$ (2b)

Putting these into matrix form,

$\left[\begin{array}{cc}1/2 & 1/2\,\sqrt{3}\\{\medskip}1/2\,\sqrt{3} & -1/2\end{array}\right] \left[\begin{array}{c}{\it S_1}\\{\medskip}{\it S_2}\end{array}\right] = \left[\begin{array}{c}Q\\{\medskip}P\end{array}\right]$ (3)

The inverse of the matrix is

$A^{-1}=\left[\begin{array}{cc}1/2 & 1/2\,\sqrt{3}\\{\medskip}1/2\,\sqrt{3} & -1/2\end{array}\right]$ (4)

We can see from Equations (3) and (4) that the matrix A is:

Symmetric
Orthogonal, because A^T = A^-1
Involutory, because A = A^-1

Inverting and solving for x,

$x=A^{-1}b=\left[\begin{array}{c}{\it S_1}\\{\medskip}{\it S_2}\end{array}\right]=\left[\begin{array}{cc}1/2 & 1/2\,\sqrt{3}\\{\medskip}1/2\,\sqrt{3} & -1/2\end{array}\right]\left[\begin{array}{c}Q\\{\medskip}P\end{array}\right]=\left[\begin{array}{c}1/2\,Q+1/2\,\sqrt{3}P\\{\medskip}1/2\,\sqrt{3}Q-1/2\,P\end{array}\right]$ (5)