This is an example of computation of a 2D moment computation. The example itself is from Movnin and Izrayelit (1970). First, however, we will give some background on this problem, from Targ (1988):


With that out of the way, we can consider the problem itself, which is shown below.
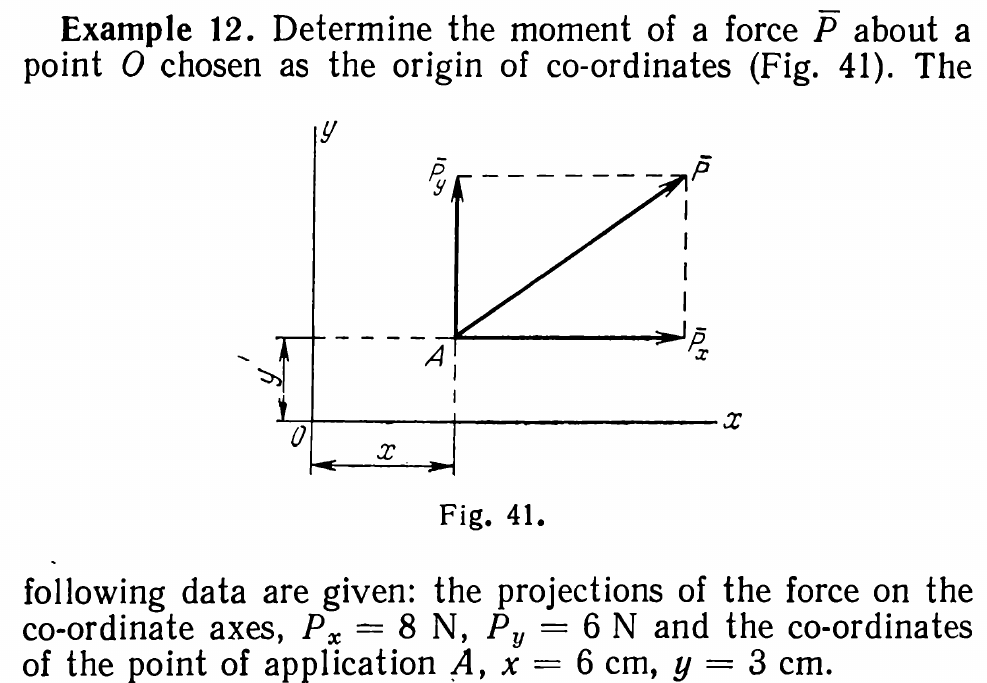
Unfortunately the solution given in the source is not correct. We will consider three ways of solving this problem. The first two are shown in the diagram below.
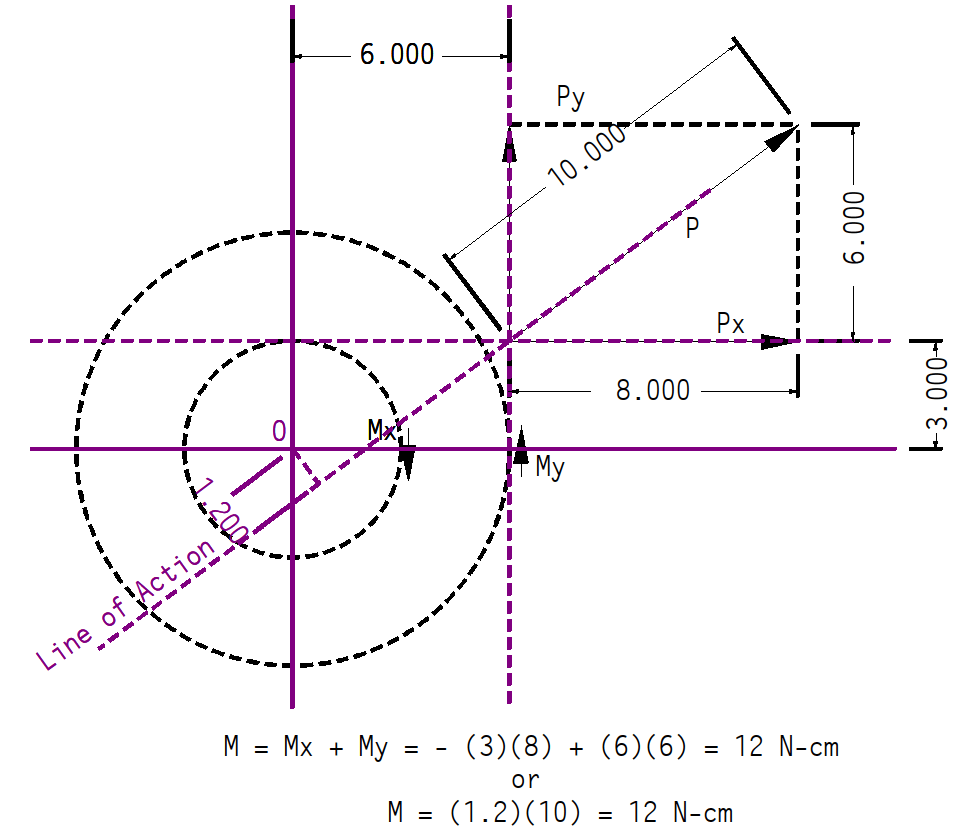
As noted earlier, the moment of any force is the perpendicular (shortest) distance between the force itself. This can be seen above; the line of action is extended downward and its closest point to the origin is 1.2 cm. Since the total force is 10 N, the moment is (1.2)(10) = 12 N-cm.
From a graphical standpoint, this is ideal; however, it is not always simple to get to this result without a graphical analysis. The alternative is to take the moments of the x- and y-components of the force times the perpendicular distance from each of these to the center of the moment. This is shown above, where we have two moments (Mx and My) which we add together. Counterclockwise moments are positive, so it is My – Mx = 12 N-cm as before.
The third technique is to use formal vector algebra; the moment is the determinant of the cross product, thus

This result is identical with the above. The moment is in the z-direction and out of the x-y plane, as we would expect.